|
| Peter Felix Schuster* | | | | | Zivilprozessuale Berechnungen mit Mitteln der objektorientierten Programmierung bewältigen - Am Beispiel der Baumbach'schen Kostenformel in Java™ | | | JurPC Web-Dok. 189/2014, Abs. 1 - 54 | | | | |
| | | Bei Referendaren und Praktikern gleichermaßen
unbeliebt sind solche Kostenberechnungen, welche die
Nebenentscheidung komplizierter als die Entscheidung in der
Hauptsache machen. Die Rede ist insbesondere von der
Baumbach'schen Kostenformel. Nach dieser selbst von ihren
Kritikern anerkannten Regel sind die Gerichtskosten und
außergerichtlichen Kosten von Streitgenossen bei
unterschiedlicher Höhe der Beteiligung oder des Erfolges am
Rechtsstreit zu verteilen. Die Berechnung ohne technische
Hilfsmittel kann je nach Anzahl der Prozessrechtsverhältnisse
und ihres Ausgangs einfach bis sehr aufwendig werden. Deshalb wurden
bereits frühzeitig Berechnungsprogramme entwickelt,[1] die allerdings in Zeiten knapper
Kassen in der Justiz nicht mehr flächendeckend eingesetzt
werden. Es lohnt sich schon deshalb zu untersuchen, wie ein solches
juristisches Problem in einer objektorientierten, einfach zu
erlernenden und frei verfügbaren Programmiersprache wie
beispielsweise Java™ zeitsparend bewältigt werden kann.
Dieser Beitrag geht zunächst kurz auf die Strukturen der
Baumbach'schen Kostenformel ein (I.) und erklärt
schematisch die Vorgehensweise (II.), um diese dann anhand der
Technik der objektorientierten Programmierung (III.) in einen
Ablaufplan zu übersetzen (IV.) und letztlich deren Umsetzung in
Java-Code (V.) vorzuschlagen. | Abs. 1 | | I. Die Baumbach'sche Kostenformel | Abs. 2 | | Anlass für die Entwicklung der Baumbach'schen
Formel ist die Erkenntnis, dass die gesetzliche Regelung des §
100 ZPO die Kostenverteilung bei einer Streitgenossenschaft im Sinne
der § 59 ff. ZPO nur unvollständig regelt: Erfasst ist nur
der Fall, dass alle Streitgenossen gleichmäßig
unterliegen. Zudem steht jeder Beteiligte nur mit seinem jeweiligen
Prozessgegner, nicht aber mit seinem Streitgenossen in einem
Prozessrechtsverhältnis, und nur im
Prozessrechtsverhältnis darf eine Kostenhaftung ausgesprochen
werden.[2] Das
berücksichtigt die Baumbach'sche Formel zum einen dadurch,
dass die Verteilung der Gerichtskosten und der
außergerichtlichen Kosten jedes Beteiligten getrennt erfolgt.
Andererseits ist zu berücksichtigen, dass ein Kläger, der
mehrere Beklagte in Anspruch nimmt, jeweils einen Angriff gegen
jeden der Streitgenossen führt und schon dann teilweise
unterliegt, wenn er nicht gegen alle Streitgenossen vollständig
obsiegt. Um ein Unterliegen gegen einen der Streitgenossen als
Teilunterliegen in der Kostenquotelung berücksichtigen zu
können, muss bei Anwendung der Baumbach'schen Formel ein
sogenannter fiktiver Streitwert berechnet werden, der sich mit jedem
einzelnen Angriff erhöht. Die Quote der Gerichtskosten ergibt
sich aus dem Verhältnis des jeweiligen Unterliegens zum
fiktiven Streitwert. Ähnliches gilt für die Berechnung der
Verteilung der jeweiligen außergerichtlichen Kosten: Kein
Beteiligter darf zur Tragung der Kosten eines seiner Streitgenossen
verurteilt werden; stattdessen muss hier der fiktive Streitwert aus
der Summe derjenigen Prozessrechtsverhältnisse angesetzt
werden, an denen die jeweils erstattungsberechtigte Partei beteiligt
ist; jede andere Partei, die mit dem Beteiligten in einem
Prozessrechtsverhältnis steht, muss dann einen Anteil der
außergerichtlichen Kosten je nach ihrem Unterliegen im
Verhältnis zu diesem speziellen fiktiven Streitwert tragen.[3] | Abs. 3 | | Hier bietet sich eine Tabelle an, um die einzelnen
Angriffe, die einzelnen Verluste und Gesamtverluste darzustellen und
daraus die jeweilige Quote zu berechnen. In jede Zeile ist dabei ein
Einzelangriff einzutragen und in jeder Spalte die Verluste des
jeweiligen Kostenschuldners, wobei gesamtschuldnerisch in Anspruch
genommene Streitgenossen als ein (zusätzlicher) Schuldner
behandelt werden, soweit sie gesamtschuldnerisch verurteilt werden.
In einer weiteren Zeile werden bei jedem der Kostenschuldner die
jeweiligen Verluste summiert, um diese in der letzten Zeile ins
Verhältnis zum fiktiven Streitwert (Kostenquote) zu
setzen. | Abs. 4 | | Dies soll an folgendem Beispiel verdeutlicht werden:[4] Der Kläger nimmt
zwei Beklagte auf gesamtschuldnerische Zahlung von 10.000,00 €
in Anspruch. Das Landgericht verurteilt beide Beklagte als
Gesamtschuldner zur Zahlung von 5.000,00 €, den Beklagten zu 1)
darüber hinaus zur Zahlung weiterer 2.500,00 €. In
Tabellenform lässt sich das folgendermaßen darstellen: | Abs. 5 |
| | Einzelangriff | Verlust des Klägers | Verlust der Beklagten als Gesamtschuldner | Verlust des Beklagten zu 1.) | Verlust des Beklagten zu 2.) | | Kläger ./. Beklagter zu 1.) (10.000,00 €) | 2.500,00 € | 5.000,00 € | 2.500,00 € | - | | Kläger ./. Beklagter zu 2.) (10.000,00 €) | 5.000,00 € | 5.000,00 € | - | 0,00 € | | Summe der Verluste | 7.500,00 € | 10.000,00 € | 2.500,00 € | 0,00 € | | Quote, bezogen auf fiktiven Streitwert 20.000,00 € | 37,5 % | 50 % | 12,5 % | - | | | | Die in der letzten Zeile ermittelte Quote bezieht sich
auf die Gerichtskosten. Die Quoten für die
außergerichtlichen Kosten der einzelnen Parteien können
anhand derselben Tabelle berechnet werden, indem für die
jeweilige Partei nur die Einzelangriffe (Zeilen) berücksichtigt
werden, an denen sie beteiligt ist. Die gesamtschuldnerischen
Verluste, die die Partei mittragen muss, werden ihren eigenen
Verlusten hinzugerechnet. Für den Kläger ergeben sich hier
dieselbe Tabelle und damit dieselbe Quotelung wie für die
Gerichtskosten, da er an allen Einzelangriffen beteiligt ist.
Für die Kosten des Beklagten zu 1.) wäre hingegen nur die
erste Zeile mit dem gegen ihn gerichteten Angriff des Klägers
zu berücksichtigen, wobei die Verluste ins Verhältnis zum
Einzelstreitwert 10.000,00 € für diesen Einzelangriff zu
setzen sind. Für die außergerichtlichen Kosten des
Beklagten zu 1.) ergibt sich, dass er selbst 75% (2.500,00 €
alleiniger Verurteilung + 5.000,00 € seiner
gesamtschuldnerischen Verurteilung in Relation zu 10.000,00 €),
der Kläger 25% und der an diesem Angriff nicht beteiligte
Beklagte zu 2.) nichts zu tragen hat. Nach denselben
Maßstäben ergibt sich für die
außergerichtlichen Kosten des Beklagten zu 2.), dass er selbst
50% (5.000,00 € seiner gesamtschuldnerischen Verurteilung :
10.000,00 € Einzelstreitwert) und der Kläger die
übrigen 50% tragen muss; der zwar an der gesamtschuldnerischen
Verurteilung in der Hauptsache, nicht aber an diesem Einzelangriff
beteiligte Beklagte zu 1.) hat dem Beklagten zu 2.) als seinem
Streitgenossen nichts zu erstatten. | Abs. 6 | | II. Schematische Beschreibung des Vorgehens | Abs. 7 | | Wenn man diese Ausführungen zusammenfasst, geht der
Jurist bei der Berechnung mittels einer solchen Tabelle also recht
schematisch vor. Wollte man dies als „Kochrezept" einem
befreundeten anderen Juristen erklären, würde dies
letztlich aus folgenden Arbeitsanweisungen bestehen: | Abs. 8 | | Nimm eine leere Tabelle. Suche aus dem Rechtsstreit alle
einzelnen Angriffe – Zweipersonenverhältnisse – mit
dem dazugehörigen Streitwert heraus und schreibe sie
untereinander auf. Das ergibt die Zeilen bzw. deren Beschriftung.
Suche sodann alle Personen oder Personenmehrheiten heraus, die als
solche potenziell in einem dieser Angriffe einen Verlust erleiden
könnten, sei es als Verurteilung (bei Beklagten), sei es, weil
ihr Anliegen nicht vollständig durchdringt (beim Kläger).
Schreibe diese nebeneinander auf – sie ergeben die Spalten
bzw. deren Überschriften. Gehe sodann nacheinander die Angriffe
(Zeilen) durch und in der jeweiligen Zeile dann alle
Personen/Personenmehrheiten (Spalten). Schreibe in die jeweilige
Tabellenzelle, wie viel Verlust (in EUR) die jeweilige
Person(enmehrheit) bei dem jeweiligen Einzelangriff erlitten hat.
Danach rechne die Summe der Spalten zu den Gesamtverlusten für
die jeweilige Person/Personenmehrheit und die Summe der Streitwerte
zum fiktiven Streitwert zusammen. Die jeweilige Quote lässt
sich errechnen, indem für jede Spalte die zuvor ermittelte
Verlustsumme ins Verhältnis zum fiktiven Streitwert gesetzt
wird. | Abs. 9 | | Von diesem „Rezept" ausgehend, sollen unter III.
detaillierte Überlegungen zum Programmablauf angestellt werden.
Zuvor geht der nächste Abschnitt aber auf die Grundzüge
der objekt-orientierten Programmierung ein. | Abs. 10 | | III. Objekt-orientierte Programmierung | Abs. 11 | | Um die Umsetzung dieses Vorgehens in Java™ zu
planen, muss in diesem Abschnitt in die sogenannte objektorientierte
Programmierung eingeführt werden. | Abs. 12 | | Die objektorientierte Programmierung (kurz: OOP) basiert
auf dem Gedanken der Objektorientierung, der seinerseits komplexe
Systeme durch das Zusammenspiel von kooperierenden Objekten
beschreibt. Der Begriff des Objekts ist dabei – ähnlich
dem „etwas" im Bereicherungsanspruch – bewusst weit
gefasst und nur dadurch umgrenzt, dass es Eigenschaften (Attribute)
hat und Methoden bereitstellt; es muss dabei nicht
gegenständlich sein.[5] Die Programmierung richtet sich dabei ihrer Grundidee
nach „an den Grundstrukturen desjenigen Teils der Wirklichkeit
(aus), der die gegebene Anwendung betrifft".[6] | Abs. 13 | | Eng verknüpft mit den Objekten sind die Klassen
oder Typen. Diese stellen eine Abstraktion verschiedener
gleichartiger Objekte des betrachteten Teils der Wirklichkeit dar,
und definieren die Eigenschaften, anhand derer eine einzelne Instanz
der Klasse (das eigentliche Objekt) zu beschreiben ist, sowie die
bereitgestellten Methoden, die dann im Programm bei jeder Instanz
der Klasse zur Verfügung stehen. Mit den Methoden seiner Klasse
kann das Objekt dann z.B. seine Eigenschaften verändern, den
Wert einer Eigenschaft zurückliefern, Berechnungen anstellen
und vielerlei mehr. Durch Kapselung wird die innere Implementierung
(also die konkrete programmmäßige Umsetzung einer
Klassenbeschreibung) von äußerem Zugriff abgeschirmt, so
dass der Zugriff nur über die definierten Schnittstellen (z.B.
öffentliche Methoden) möglich ist. Klassen können von
einer anderen Klasse dergestalt abgeleitet werden, dass die
abgeleitete Klasse (Kindklasse, Unterklasse oder Subklasse) von der
anderen Klasse (Elternklasse, Basisklasse, Oberklasse oder
Superklasse) deren Datenstruktur (Eigenschaften / Attribute) oder
Methoden „erbt" – man spricht daher von
„Vererbung". [7] | Abs. 14 | | Um beispielsweise einen Bereich des Zivilprozesses in
die Welt der OOP zu übertragen, könnte man sich die
Handelnden im Prozess abstrahiert als Klasse
„Prozessbeteiligter" vorstellen, mit den Eigenschaften Name,
Rolle (im Prozess) und Anrede sowie den Methoden Laden, Erscheinen
und Aussagen/Vortragen. Man könnte sich zusätzlich die
Unterklasse „Kläger" vorstellen, die von der Oberklasse
„Prozessbeteiligter" all deren Eigenschaften erbt und
zusätzlich die Methode „klagen" und die Eigenschaft
„Klageantrag" bereitstellt. | Abs. 15 | | In der Programmierung, nicht nur in der
objekt-orientierten Programmierung, wird stets versucht, ein
komplexes Problem in mehrere Teilprobleme zu zerlegen („Teile
und herrsche", lat. „divide et impera"). Dadurch sinkt
häufig der jeweilige Lösungsaufwand. Außerdem kann
man ausgegliederte Routinen zur Lösung des Teilproblems
häufig an mehreren Stellen des Programms verwenden. So
vermeidet man, denselben Programmcode an mehrere Stellen des
Programms kopieren und einfügen (und pflegen) zu müssen.[8] Das geschieht einmal
dadurch, die schon beschriebenen Methoden möglichst kleinteilig
zu halten, so dass jede nur ein Teilproblem behandelt. Um bei
Wiederholungen Programmanweisungen nicht mehrfach aufschreiben zu
müssen, bieten alle Programmiersprachen außerdem
sogenannte „Schleifen" (engl. „loop"). [9] Damit ist der Befehl gemeint,
eine oder mehrere Anweisungen x-mal zu wiederholen (einfache
„for"-Schleife mit Index) bzw. für alle Elemente einer
Sammlung zu wiederholen (erweiterte „for"-Schleife).[10] | Abs. 16 | | IV. Überlegungen zum Ablauf | Abs. 17 | | Vor dem Verfassen des eigentlichen Programmcodes stellt
ein Programmierer Überlegungen an, wie die Programmlogik und
Datenstruktur auszusehen hat. Hier sollen zunächst einige der
gebrauchten Klassen vorgestellt und dann der Programmablauf der
Quotenberechnung in einem sogenannten Pseudocode – d.h. der
Veranschaulichung des Programmablaufs in nahezu natürlicher,
maschinenunabhängiger Sprache[11] – vorformuliert werden. Letztlich
soll das oben unter II. skizzierte „Kochrezept" in eine
programmiertaugliche Vorstufe übertragen werden. Um den Rahmen
des Artikels nicht zu sprengen, sei hier nur der Programmablauf bei
einem Kläger gegenüber mehreren Beklagten, ohne
Widerklagen und nur bezüglich der Verteilung der
Gerichtskostenquoten beschrieben. | Abs. 18 | | Zur Berechnung werden außer der Klasse, die den
eigentlichen Programmkern enthält (diese heißt in unserem
Fall BaumbachFormel und wird später beim Pseudocode
beschrieben), Daten zu den am Prozess beteiligten Parteien
benötigt. Hierin können auch Angaben zum Streitwert der
Angriffe und deren Erfolg gespeichert werden. | Abs. 19 | | 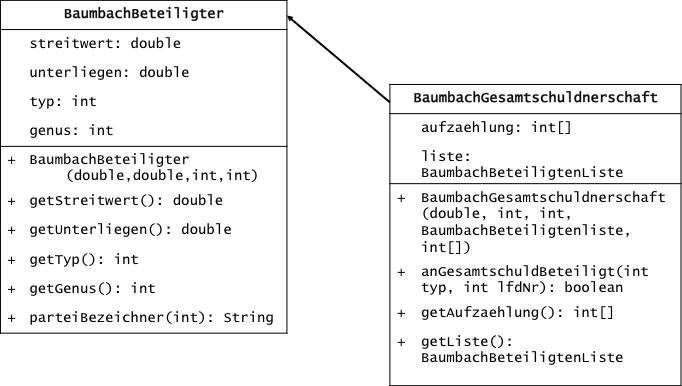 | Abs. 20 | | Die grundlegende Klasse BaumbachBeteiligter soll genau
dies umsetzen: Sie umfasst den Beteiligtentyp (Kläger oder
Beklagter), der hier als Ganzzahl (engl. „integer" oder kurz
„int") mit „0" bzw. „1" angegeben wird, das Genus
des Beteiligten ebenfalls als Ganzzahl (0 = männlich, 1 =
weiblich), den Streitwert des Angriffs gegen diesen Beteiligten und
das Unterliegen des Beteiligten bei diesem Angriff, als
Fließkommazahl mit doppelter Genauigkeit („double"). Die
Variablen „unterliegen" und „streitwert" sind beim
Kläger immer 0,00 EUR, da Widerklagen außer Betracht
bleiben. Für alle vorgenannten Werte („Feld") sind
sogenannte „Getter"-Methoden vorhanden, d.h. eine Methode, die
den Wert des gleichnamigen Felds zurückgibt: die Methode
„getUnterliegen()" gibt den Wert des Felds „unterliegen"
an den aufrufenden Programmabschnitt zurück. Die Werte werden
der Klasse bereits bei der Erzeugung der Instanz übergeben, was
mit einem sogenannten „Konstruktor", d.h. einer speziellen
Methode[12] zusammen
mit dem Operator „new" geschieht, z.B. „new
BaumbachBeteiligter(int typ, int genus, double streitwert, double
unterliegen)". Daneben ist eine Methode „parteiBezeichner"
implementiert, die für die Tenorerzeugung die Parteibezeichnung
in der richtigen Beugeform als Zeichenkette („String")
zurückgibt, z.B. „der Kläger", „des
Klägers" usw. | Abs. 21 | | Von der Klasse BaumbachBeteiligter (Oberklasse) wird die
Klasse BaumbachGesamtschuldnerschaft abgeleitet. Diese Klasse
verkörpert die gesamtschuldnerischen Verurteilungen, die in
einigen Gesichtspunkten wie Beteiligte behandelt werden können:
In der oben gezeigten Tabelle ist für das gesamtschuldnerische
Unterliegen eine Spalte vorgesehen, auch in einem Tenor wird von der
vollständigen Gesamtschuldnerschaft wie von einer Partei
gesprochen („die Beklagten zu 1) und 2) werden
verurteilt..."). Sie erbt alle Felder und Methoden ihrer Oberklasse,
wobei die Methode parteiBezeichner mit einer spezielleren Methode
überschrieben wird. Zusätzlich werden Felder und Methoden
benötigt, mit denen die Klasse speichern und verwerten kann,
dass mehrere tatsächliche Beteiligte (und welche) verurteilt
worden sind. Dazu wird einmal die BaumbachBeteiligtenListe
„liste" benötigt: in diesem Typ können alle
Beteiligten des Prozesses übergeben und mit ihren als Ganzzahl
(int) vergebenen Ordnungsziffern (0, 1 ... n) angesprochen werden;
diese Klasse wird im nächsten Absatz näher erläutert.
Zum anderen werden im Feld „aufzaehlung" diejenigen Ganzzahlen
gespeichert, die angeben, welche Beteiligten der „liste" an
der Gesamtschuldnerschaft beteiligt, z.B. 0, 1 und 3, wenn die
Beklagten zu 1, 2 und 4 gesamtschuldnerisch verurteilt wurde (in
Java wird meist von 0 an gezählt). Der Speichertyp ist hier ein
„Array"[13],
also eine Aneinanderreihung mehrerer Variablen desselben Typs, hier
von int. Statt zwei Felder zu nehmen („liste" und
„aufzaehlung"), könnte die „liste" direkt nur mit
den gesamtschuldnerisch verurteilten Beteiligten bestückt
werden. Für die Gestaltung der Programmoberfläche ist das
gewählte Vorgehen jedoch einfacher: so kann die Oberfläche
immer die Gesamtliste der Beteiligten übergeben und muss sie
nicht für jede gesamtschuldnerische Verurteilung neu zusammen
setzen. | Abs. 22 | | 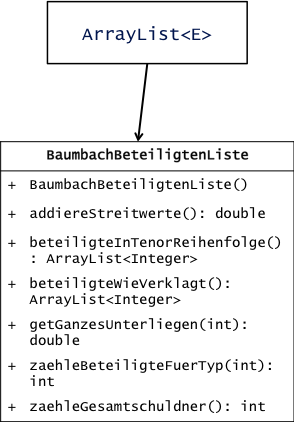 | Abs. 23 | | Die Klasse BaumbachBeteiligtenListe hingegen wird von
einer Java-eigenen Klasse „ArrayList" abgeleitet. Dieser Typ
verhält sich ähnlich dem oben beschriebenen Array, kann
jedoch beliebig mit weiteren Elementen erweitert werden, wohingegen
ein Array immer die bei Initialisieren angegebene Anzahl der
Elemente behält.[14] Elemente aus der ArrayList können mit der Methode
get(int index) abgefragt werden, neue Elemente mit der Methode add(E
element) am Ende der Liste hinzugefügt werden. Die Klasse
BaumbachBeteiligtenListe selbst übernimmt die Verwaltung der
Beteiligten und der Gesamtschuldnerschaften. Eine solche Liste dient
vor allem als sogenanntes Parameterobjekt, also ein Objekt, das
genau die von einer Klasse benötigten Werte strukturiert
abbildet, mit dem dann die Programmoberfläche Werte der Klasse
BaumbachFormel übergibt. Hier fasst die
BaumbachBeteiligtenListe alle Beteiligten zusammen, mit denen dann
die Hauptklasse BaumbachFormel arbeiten soll. Zudem stellt die
Klasse BaumbachBeteiligtenListe einige Methoden bereit, mit der die
enthaltenen Beteiligten nach vordefinierten Kriterien (z.B. alle
Gesamtschuldnerschaften oder alle „wirklichen" Beteiligten)
aufgefunden oder in eine bestimmte Reihenfolge (z.B. die für
die Tenorierung benötigte) gebracht werden können. Daneben
benötigt die Klasse BaumbachFormel bestimmte
Berechnungsoperationen, die in BaumbachBeteiligtenListe besser
angesiedelt sind, z.B. die Summe aller Streitwerte zur Berechnung
des fiktiven Streitwerts und das vollständige Unterliegen eines
„echten" Beteiligten unter Berücksichtigung aller
Gesamtschuldnerschaften, denen er angehört. | Abs. 24 | |  | Abs. 25 | | Der Kern der Berechnung liegt aber in der Klasse
BaumbachFormel. Beim Erzeugen über den Konstruktor wird diesem
eine BaumbachBeteiligtenListe übergeben und als Feld
baumbachBeteiligtenListe im Speicher abgelegt. Die Methode
ermittleGerichtskostenQuoten zur Berechnung nach der
Baumbach'schen Formel im Stil der oben dargestellten Tabelle
soll hier in einem Pseudocode näher betrachtet werden. | Abs. 26 | | Zunächst müssen alle in der gesamten Methode
gebrauchten Variablen deklariert – d.h. dem Compiler bekannt
gemacht – und, sofern möglich, bereits mit einem
Startwert initialisiert werden. Variablen hingegen, die nur für
einen Schleifendurchlaufbenötigt werden, werden innerhalb der
Schleife initialisiert (s.u., 2.). | Abs. 27 | | Drei ArrayLists anlegen: ArrayList<double()>
namens angriffsListe anlegen; diese enthält ein double-Array
für jede Zeile der Baumbach-Tabelle; | Abs. 28 | | zusätzlich eine ArrayList<Integer>
beteiligteWieVerklagt (ergibt die Zahl der Angriffe: je eine Zeile
für jeden „echten" Beklagten); | Abs. 29 | | und eine ArrayList<Integer>
beteiligteInTenorReihenfolge (je eine Spalte für jede Partei
und jede Gesamtschuldnerschaft) für die Spalten (beides wird
von der baumbachBeteiligtenListe geliefert); | Abs. 30 | | weiter eine double fiktiverStreitwert; | Abs. 31 | | ein Array double() quoten, in dem zum Schluss die Quote
jeder Partei abgelegt wird und ein Array double() verluste, deren
Elemente zunächst jeweils mit 0.0 initialisiert werden. 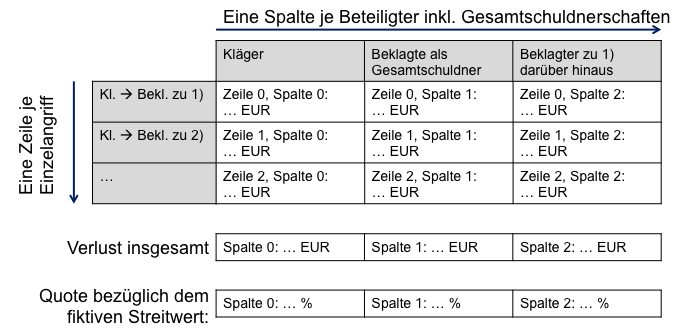 | Abs. 32 | | In der oben vorgestellten Tabelle stehen die
Einzelverluste der jeweils in der Spaltenüberschrift benannten
Partei oder Gesamtschuldnerschaft. Diese soll das Programm anhand
von zwei Schleifen bestimmen, die ineinander verschachtelt sind.
Für das Berechnen der Quoten nach Baumbach'scher
Kostenformel mit der genannten Tabelle soll auf zwei einfache
„for"-Schleifen zurückgegriffen werden. Diese sollen alle
Zeilen durchlaufen, in jeder Zeile alle Spalten füllen und
dabei über jeweils einen Index auf Zeile und Spalte zugreifen.
Oder, um es als Anweisung zu sagen: „berechne Spalte y in
Zeile x und wiederhole es für jede Spalte in der Zeile und das
ganze für alle Zeilen": | Abs. 33 | | Eine äußere Schleife zählt die Zeilen
durch, eine Zeile für jeden Angriff. BaumbachBeteiligter a
(lokale Variable) ist der, gegen den sich der Angriff richtet.
Für jede Zeile ein Array double() werte anlegen mit so vielen
Elementen wie Spalten anhand von beteiligteInTenorReihenfolge. | Abs. 34 | | Darin verschachtelt zählt eine innere Schleife die
Spalten durch, eine für jede Partei inkl.
Gesamtschuldnerschaften. BaumbachBeteiligter (Partei oder
Gesamtschuldnerschaft) b ist die, deren Verlust (lokale Variable
„wert") berechnet werden soll. Dabei werden folgende
Wenn-/Dann-Abfragen durchgeführt: | Abs. 35 | | i. Wenn a ein Beklagter und b der Kläger ist, dann
wert = a.streitwert – a.unterliegen. | Abs. 36 | | ii. Wenn ansonsten a ein Beklagter ist und b == a
à wert = b.unterliegen. | Abs. 37 | | iii. Wenn ansonsten a ein Beklagter, b eine
Gesamtschuldnerschaft und a in b enthalten ist à wert =
b.unterliegen. | Abs. 38 | | iv. Sonst: wert = 0.0. | Abs. 39 | | Jeweils wird fiktiverStreitwert um a.streitwert,
verlustSumme(spalte) um b.unterliegen erhöht und werte(spalte)
= wert gesetzt. | Abs. 40 | | Am Ende jedes Durchgangs der äußeren Schleife
wird das Array werte der angriffsListe hinzugefügt. | Abs. 41 | | Wenn die Schleifen abgearbeitet worden sind, wird in
einer neuen Schleife über die Spalten jeweils quoten(spalte) =
verluste(spalte) / fiktiverStreitwert * 100.0 errechnet. | Abs. 42 | | Danach das Array verluste und das Array quoten der
angriffsListe hinzufügen. | Abs. 43 | | Die ArrayList angriffsListe als Ergebnis
zurückgeben. | Abs. 44 | | V. Umsetzung in Java™ | Abs. 45 | | Die hier im Folgenden verwendete Programmiersprache
Java™ [15] ist
keine „reine„ objekt-orientierte Programmiersprache,
sondern gebraucht auch Anteile anderer Paradigmen und auch einfache
Typen wie „int„, die keine Objekte sind. Zudem werden
keine selbstständig ausführbaren Programme erzeugt,
sondern die Applikationen erfordern auf dem ausführenden
Rechner immer noch eine Laufzeitumgebung. Java zeichnet sich jedoch
durch leichte Erlernbarkeit und hohe Verbreitung aus. Bei Problemen
findet man leicht Antworten und freie Zusatzpakete bei der aktiven
„Community„ im Internet; unter den zahlreichen
Programmierern mit Java-Kenntnissen findet man vielleicht sogar am
Projekt interessierte Mitstreiter. Für Java™ sprechen
zudem die hohe Sicherheit und ein plattformübergreifender
Ansatz,[16" href="#fn15) ist keine „reine„
objekt-orientierte Programmiersprache, sondern gebraucht auch
Anteile anderer Paradigmen und auch einfache Typen wie
„int„, die keine Objekte sind. Zudem werden keine
selbstständig ausführbaren Programme erzeugt, sondern die
Applikationen erfordern auf dem ausführenden Rechner immer noch
eine Laufzeitumgebung. Java zeichnet sich jedoch durch leichte
Erlernbarkeit und hohe Verbreitung aus. Bei Problemen findet man
leicht Antworten und freie Zusatzpakete bei der aktiven
„Community" im Internet; unter den zahlreichen Programmierern
mit Java-Kenntnissen findet man vielleicht sogar am Projekt
interessierte Mitstreiter. Für Java™ sprechen zudem die
hohe Sicherheit und ein plattformübergreifender Ansatz, [16] ist keine
„reine„ objekt-orientierte Programmiersprache, sondern
gebraucht auch Anteile anderer Paradigmen und auch einfache Typen
wie „int", die keine Objekte sind. Zudem werden keine
selbstständig ausführbaren Programme erzeugt, sondern die
Applikationen erfordern auf dem ausführenden Rechner immer noch
eine Laufzeitumgebung. Java zeichnet sich jedoch durch leichte
Erlernbarkeit und hohe Verbreitung aus. Bei Problemen findet man
leicht Antworten und freie Zusatzpakete bei der aktiven
„Community" im Internet; unter den zahlreichen Programmierern
mit Java-Kenntnissen findet man vielleicht sogar am Projekt
interessierte Mitstreiter. Für Java™ sprechen zudem die
hohe Sicherheit und ein plattformübergreifender
Ansatz,[16">[15) ist keine „reine" objekt-orientierte
Programmiersprache, sondern gebraucht auch Anteile anderer
Paradigmen und auch einfache Typen wie „int", die keine
Objekte sind. Zudem werden keine selbstständig
ausführbaren Programme erzeugt, sondern die Applikationen
erfordern auf dem ausführenden Rechner immer noch eine
Laufzeitumgebung. Java zeichnet sich jedoch durch leichte
Erlernbarkeit und hohe Verbreitung aus. Bei Problemen findet man
leicht Antworten und freie Zusatzpakete bei der aktiven
„Community" im Internet; unter den zahlreichen Programmierern
mit Java-Kenntnissen findet man vielleicht sogar am Projekt
interessierte Mitstreiter. Für Java™ sprechen zudem die
hohe Sicherheit und ein plattformübergreifender Ansatz,[16] d.h. die erzeugten
Applikationen können auf verschiedenen Betriebssystemen wie
Windows™, Linux und Mac OS X und sogar einigen
Betriebssystemen für Mobilgeräte gestartet werden. Einfach
zu erlernen und weit verbreitet sind auch Programmiersprachen
für das Dot-NET-Framework von Microsoft wie etwa
VisualBasic.NET[17] oder – schon komplexer – C#. Hiermit würde man zwar
selbstständig ausführbare Programme erzeugen, sich aber
auf eine Plattform (hier: Microsoft Windows™) festlegen, was
man mit Java™ vermeidet. Plattformübergreifend
programmieren wiederum kann man auch mit JavaScript oder den
modernen Sprachen Ruby on Rails usw. Diese richten sich jedoch
vornehmlich auf eine Nutzung im Web. Wegen der möglicherweise
sensiblen Beteiligtendaten soll hier aber eine webbasierte Nutzung
ausgeklammert werden. Zudem soll die Möglichkeit erhalten
bleiben, das Programm ohne Internet-Zugang nutzen zu können.
Somit verdiente Java™ hier den Vorzug. | Abs. 46 | | Nach den Überlegungen unter IV. könnte der
Code in Java wie folgt aussehen: | Abs. 47 | |  | Abs. 48 | |  | Abs. 49 | | VI. Fazit und Ausblick | Abs. 50 | | Manche juristischen Gedankengänge folgen der
gleichen Logik, wie sie auch der objektorientierten Programmierung
zugrunde liegen. Eine Umsetzung als Java-Applikation erleichtert
nicht nur die Berechnungsarbeit, sondern hilft auch, die eigene
Methodik zu ordnen. | Abs. 51 | | Das vollständige Programm ist bereits erstellt. Es
beherrscht die Berechnung nach Baumbach'scher Kostenformel auch
in Fallgestaltungen mit Widerklagen, bietet zur Eingabe der
Beteiligten eine einfache Oberfläche und zur Weiternutzung eine
Tenorausgabe. Daneben sind Berechnungen auch bei
Teilklagerücknahme gemäß der Quoten- und der
Mehrkostenmethode sowie eine isolierte Gebührenberechnung
möglich. Das Programm lässt sich unter http://www.kostentenor.de herunterladen. Es steht unter ständiger Fortentwicklung: die
Oberfläche soll künftig noch einfacher zu bedienen werden,
aber auch die Möglichkeit zur Eingabe komplexerer Fälle
bieten können. Das Projekt soll schließlich unter einer
geeigneten Open-Source-Lizenz freigegeben werden und sucht noch
Interessierte zur Mitprogrammierung. | Abs. 52 | |  | Abs. 53 | | 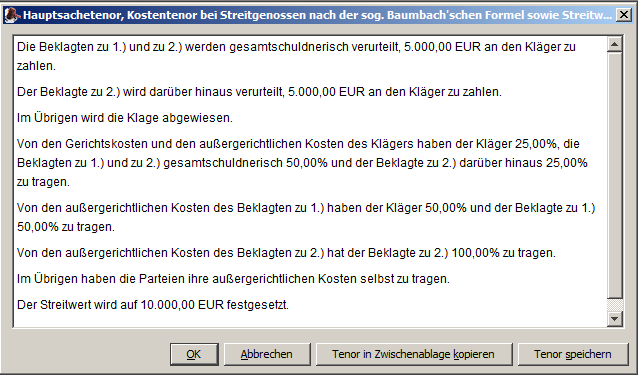 | Abs. 54 |
| | |
| | | | |
| | | | |
| | | | | Fußnoten | | | * Richter am
Landgericht in Düsseldorf (derzeit bei der
Verfahrenspflegestelle JUDICA bei der Präsidentin des
Oberlandesgerichts Düsseldorf). Der Verfasser dankt Herrn Prof.
Dr. Maximilian Herberger für die Anregung zu diesem Artikel
sowie seiner Frau, Ri.inAG Dr. Agnes Schuster, und Dipl.-Ing.
Günter Boeker für wertvolle Hinweise und Anregungen. | | [1] Dazu
Viefhues/Viefhues, „Kostenentscheidungen und
Sicherheitsleistungen im Zivilprozeß – Lösungen der
Baumbach'schen Formel mit elektronischen Hilfsmitteln", JuS 1992,
944. | | [2] Anders/Gehle, „Das Assessorexamen im Zivilrecht", 11. Aufl.
2013, A-199 ff., A-202; Gemmer, Jus 2012, 702, „Die
Baumbach'sche Kostenformel im Zivilurteil". | | [3] BGHZ 8, 325;
Anders/Gehle, Assessorexamen, A-199 ff., A-202; dies. Antrag und
Entscheidung im Zivilprozeß, Teil B, Rn. 259 ff., 260;
Baumbach/Lauterbach/Albers/Hartmann, ZPO, § 100, Rn. 52;
Gemmer, a.a.O.; Zöller-Herget, ZPO, 30. Aufl. 2014, § 100,
Rn. 5 ff. | | [4] Nach
Anders/Gehle, Assessorexamen, Rn. A-205. | | [5] Vgl.
Ullenboom, Java ist auch eine Insel, 10. Aufl. 2011 (zit. als
„Java-Insel"), Abschnitt 3.1.1; ferner dazu die
Wikipedia-Artikel http://de.wikipedia.org/wiki/Objektorientierung und http://de.wikipedia.org/wiki/Objektorientierte_Programmierung (Abruf vom 03.10.2014) | | [6] http://de.wikipedia.org/wiki/Objektorientierte_Programmierung (Abruf vom 03.10.2014) | | [7] Vgl.
Ullenboom, Java-Insel, Abschnitt 5.8; Wikipedia a.a.O. | | [8] Vgl. http://de.wikipedia.org/wiki/Teile_und_herrsche_%28Informatik%29 (Abruf vom 11.11.2014). | | [9] Vgl.
Ullenboom, Java-Insel, Abschnitt 2.6. | | [10] Vgl.
Ullenboom, Java-Insel, Abschnitt 2.6.3. | | [11] Vgl. http://de.wikipedia.org/wiki/Pseudocode (Abruf vom
12.10.2014). | | [12] Vgl.
Ullenboom, Java-Insel, Abschn. 3.4.1; http://de.wikipedia.org/wiki/Konstruktoren_und_Destruktoren (Abruf vom 21.10.2014). | | [13] Vgl.
Ullenboom, Java-Insel, Abschn. 3.8. Die Übersetzung ins
Deutsche ist „Fläche". Da diese Übersetzung nicht
besonders aussagekräftig ist und sich auch im Deutschen der
englische Ausdruck etabliert hat, wird der englische Ausdruck
eingesetzt. | | [14] Vgl. http://docs.oracle.com/javase/8/docs/api/java/util/ArrayList.html (Abruf vom 21.10.2014). | | [15] Vgl. http://www.oracle.com/technetwork/java/index.html. | | [16] Vgl. http://de.wikipedia.org/wiki/Java_%28Programmiersprache%29 (Abruf vom 12.10.2014). | | [17] Vgl.
dazu http://de.wikipedia.org/wiki/.NET. | | | | | |
| | | | |
| | | | |
| | | (online seit:
02.12.2014) | | | |
| | | Zitiervorschlag: Autor, Titel, JurPC Web-Dok,
Abs. | | | |
| | |
